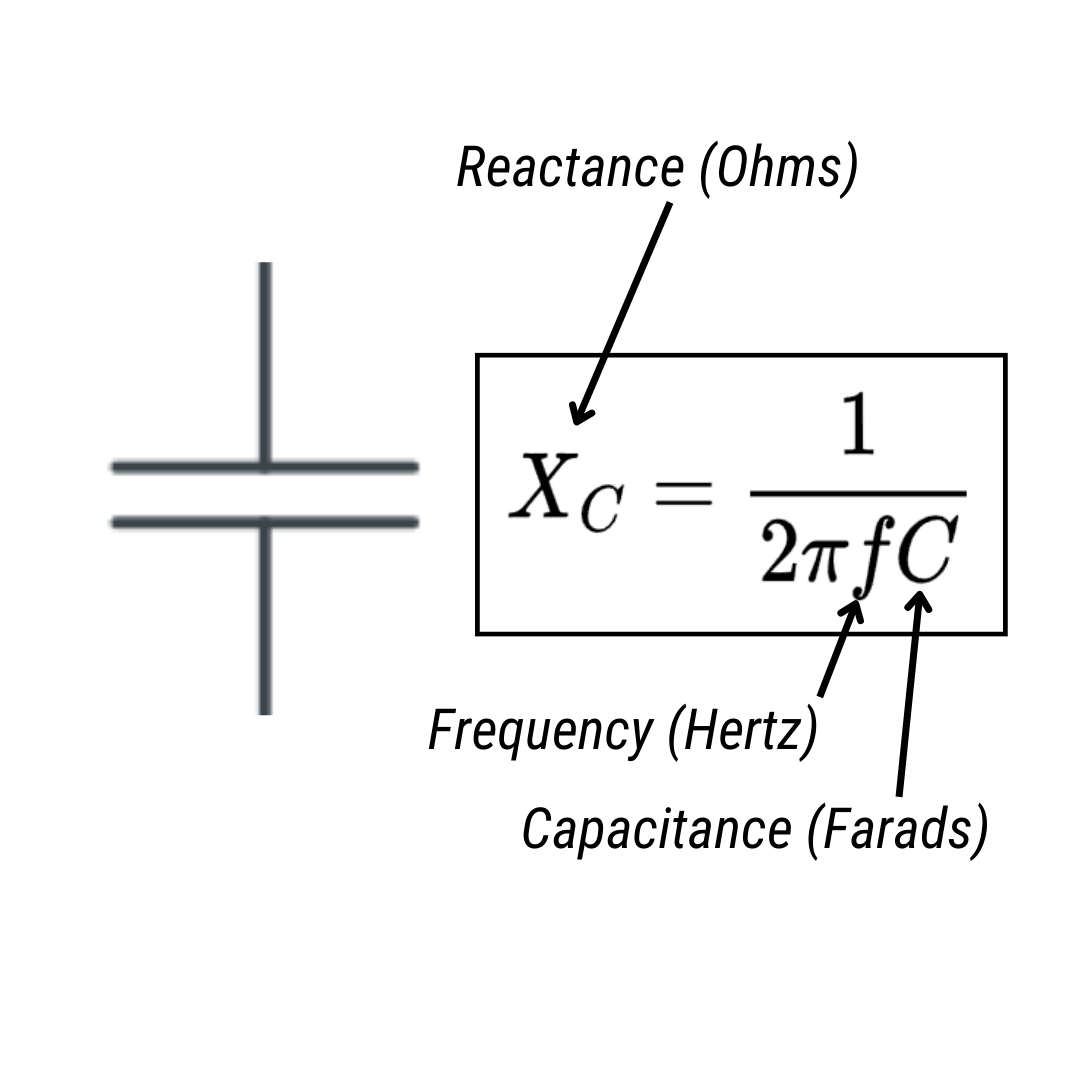
Capacitor C:
Frequency (f):
Angular Frequency (ω):
Capacitive Reactance (XC):
As a member of the Reverb Partner Program and as an Amazon Associate, StompboxElectronics earns from, and is supported by, qualifying purchases.
Capacitive Reactance (Xc) Calculator
Welcome to the Capacitive Reactance Calculator, your go-to tool for calculating the capacitive reactance of a capacitor.
Wondering how to estimate the “resistance” of a capacitor when an AC signal is applied? Look no further. We’ve got the capacitive reactance formula laid out for you below, along with a backstage pass to understanding why reactance likes to show up when alternating current takes the stage, leaving direct current out of the party.
If you’re looking for a formula for calculating RC cut-off frequencies, try out our RC filter cut-off frequency calculator. However, if you want to know how to calculate the capacitive reactance, you’re in the right place!
What is Capacitive Reactance?
Reactance, denoted as X, is an electrical circuit element’s resistance-like property that hinders the flow of current. Specifically, capacitive reactance, akin to capacitor resistance, shares the unit of Ohm (Ω). In essence, both resistance and capacitive reactance are measured in Ohms, highlighting their analogous role in opposing current flow within a circuit.
While both reactance (X) and resistance (R) may seem interchangeable in a circuit, a crucial distinction sets them apart. Reactance plays a role in impacting alternating current (AC), whereas resistance has its influence on direct current (DC). Collectively, they constitute the elements of impedance (Z), a complex quantity delineating the overall opposition a circuit poses to the flow of current.
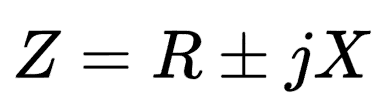
In this context, j represents an imaginary unit, denoted as (√-1), which signifies the square root of a negative number.
Capacitive reactance is a characteristic of capacitors, and inductive reactance is associated with inductors. An ideal resistor exhibits zero reactance, signifying a purely resistive element. Conversely, perfect capacitors and inductors demonstrate zero resistance.
In precise terms, the concept of capacitor resistance doesn’t exist. Typically, we use this expression as a convenient mental shorthand referring to capacitive reactance.
Calculating Capacitive Reactance
Calculate the capacitive reactance by proceeding with these steps:
- Take note of the capacitor’s capacitance (C) and the AC signal frequency (f).
- Use the capacitive reactance formula below, substituting the capacitance and frequency values. The value 3.14159 can be used in place of π.
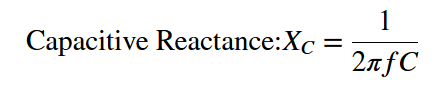
If you only have the angular frequency (ω) available to you, simply substitute 2πf for ω. The equation becomes:
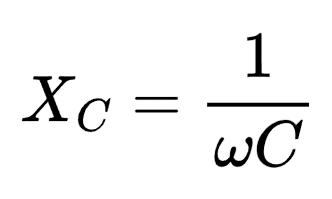
As the frequency of the AC signal increases, the capacitive reactance decreases. Does this make sense to you?
A capacitor, functioning as an energy storage device, exhibits nearly unrestricted current flow during the charging process. Higher capacity allows for more efficient passage of current. Moreover, as AC frequency increases, the capacitor has less time to fully charge itself. In the case of DC, the capacitor initially charges, but in the equilibrium state, it behaves as an open circuit.
Using the Capacitive Reactance (Xc) Calculator
First, choose which value you’d like to calculate:
- Capacitive Reactance (Xc)
- AC Signal Frequency (f)
- Capacitance (C)
The target value’s input box will color grey. The other boxes with turn green, indicating that they are ready for input.
For example, if I want to calculate the reactance of a 1uF capacitor at 1kHz then I would select the Capacitive Reactance option from the Solve for dropdown box. The reactance box turns grey and the other boxes turn green. Input the values and click Calculate. The result of 159.16 Ω appears in the reactance box.
Rules for Reactance Values
The tool only allows an integer or decimal value into the reactance field. Use the drop-down box on the side of each input box to convert the value between kilo ohms and ohms.
Rules for Capacitor Values
The tool only allows an integer or decimal value into the capacitance fields. Use the drop-down box on the side of each input box to convert the value between milliFarads, microFarads, nanoFarads, and picoFarads.
Rules for Frequency Values
Use the drop-down box on the side of the cut-off frequency input box to convert the value between Hertz, kHz, MHz, and GHz.
Meet the Author:

Hi, I’m Dominic. By day, I’m an engineer. By night, I repair and modify guitar effects! Since 2017, I’ve been independently modifying and repairing guitar effects and audio equipment under Mimmotronics Effects in Western New York. After coming out with a series of guitar effects development boards, I decided the next step is to support that community through content on what I’ve learned through the years. Writing about electronics gives me great joy, particularly because I love seeing what others do with the knowledge they gain about guitar effects and audio circuits. Feel free to reach out using the contact form!
