
[Last Updated: January 31, 2024]
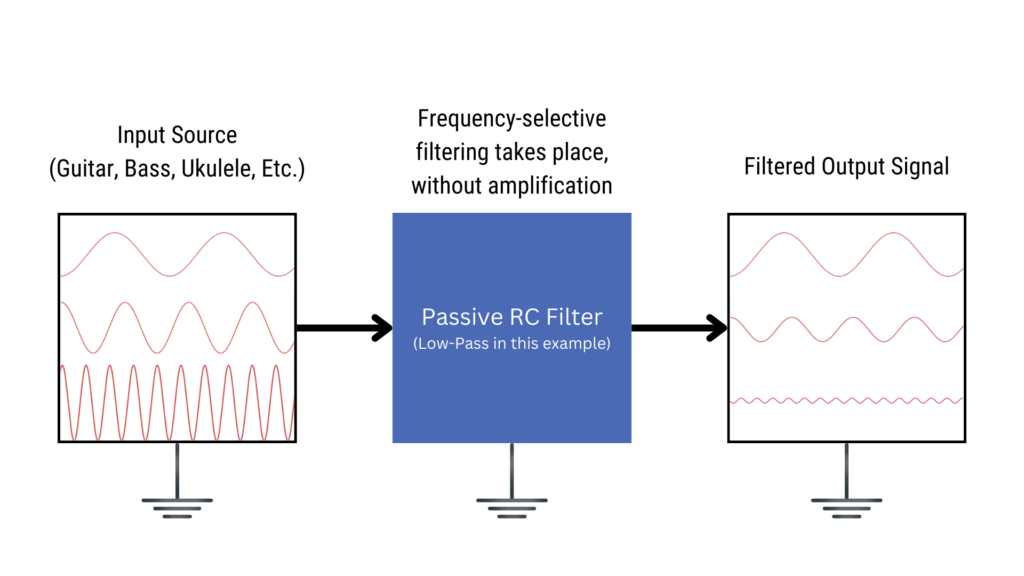
Today, we’re peeling back the curtain on Passive RC Filters! With just one resistor and one capacitor you can easily build a basic passive filter. This circuit proves useful in designing certain aspects of guitar effects pedals and helps you figure out how to modifying existing ones.
As a member of the Reverb Partner Program and as an Amazon Associate, StompboxElectronics earns from, and is supported by, qualifying purchases.
Disclaimer: Stompbox Electronics and/or the author of this article is/are not responsible for any mishaps that occur as a result of applying this content.
Introducing: Passive RC Filters
In audio electronics, passive RC filters stand as fundamental building blocks for tone-shaping. When delving into the intricacies of audio circuitry, understanding the dynamic duo of resistors and capacitors in passive RC filters becomes a crucial step toward crafting your tone.
Essentially, a passive RC filter is a circuit composed of resistors (R) and capacitors (C) working together to provide frequency filtering. In other words, these components collaborate to filter out specific frequencies, tailoring the output signal to achieve some desired tonal characteristic.
Passive vs. Active Components
The reason RC filters are called passive is because they are made up of only passive components – resistors and capacitors. Passive components do not need an external power source to work. Active components, on the other hand, do need an external power source to work properly. Examples of active components are transistors and op amps. We’ll get to those in future posts.
Types of Passive RC Filters
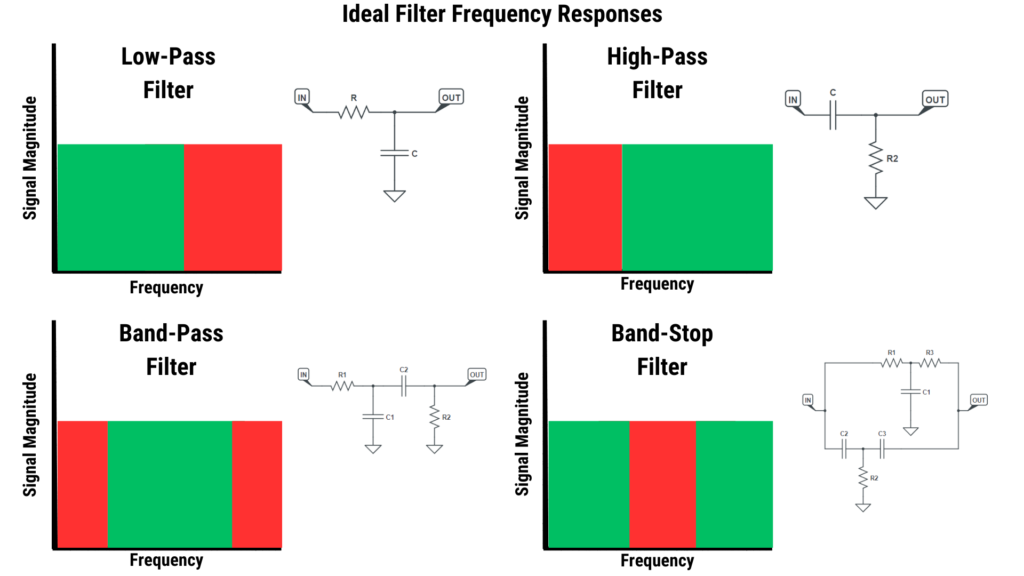
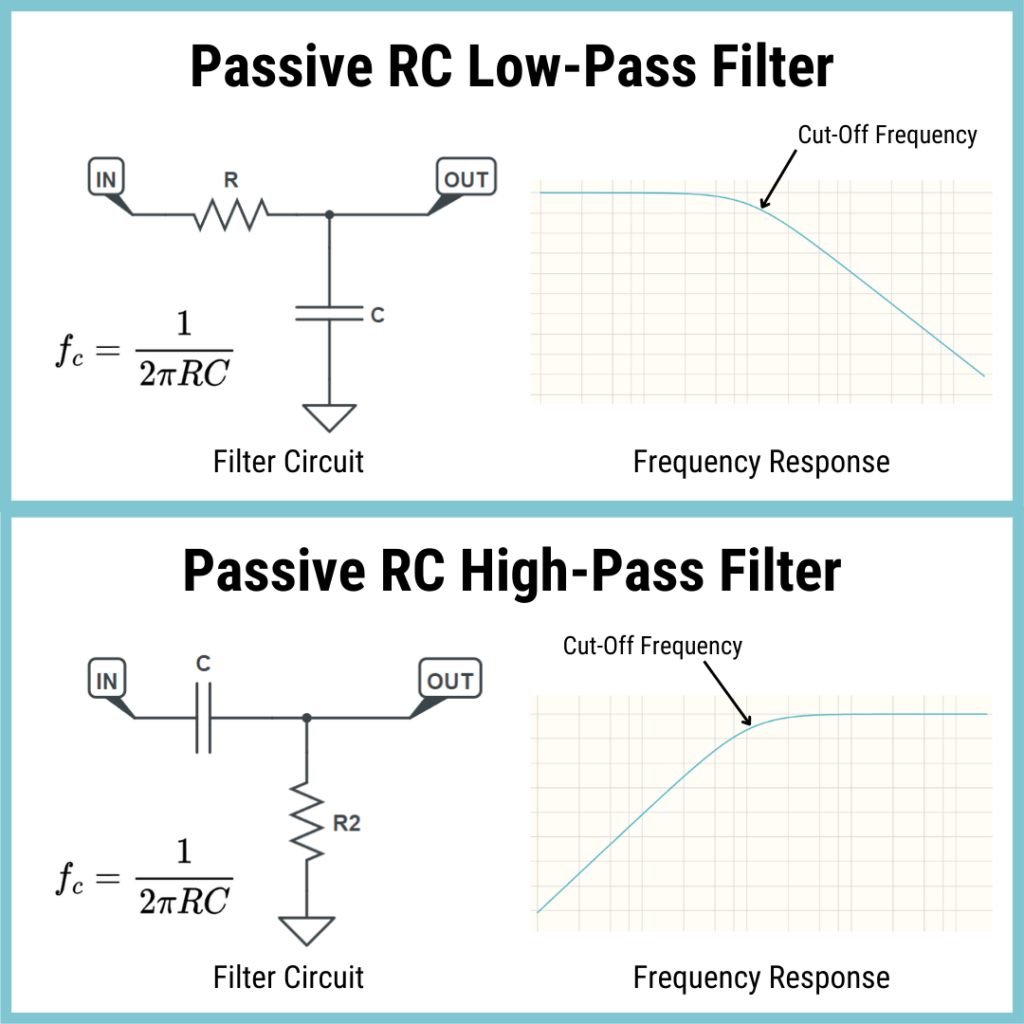
There are four main types of passive RC filters: low-pass, high-pass, band-pass and band-stop. In this article, we will only focus on low-pass and high-pass filtering, since they are the most important to understand in the context of guitar effects. See Figure 12.2 below for the ideal frequency responses of all four filter circuits, along with their basic circuit topology.
Cut-Off Frequency
Every low-pass and high-pass RC filter has a “threshold” frequency called the Cut-Off Frequency. The cut-off frequency is the point at which a filter begins significantly attenuating the input signal. It marks the boundary between the frequencies allowed to pass through relatively unaltered and those that are increasingly suppressed.
In Figure 12.2 below, ideal frequency responses are shown for each of the four types of passive RC filters. The green shades signify frequencies that are allowed to pass, while the red shades indicate frequencies that are blocked by the filter. The boundary lines that divide the green and red sections are where the cut-off frequencies are located.
For low-pass and high-pass filters there is only one cut-off frequency. Band-pass and band-stop filters have two cut-off frequencies, so two boundary lines are shown.
No Amplification
In passive RC filter circuits, there is no inherent amplification of the input signal; instead, these circuits predominantly attenuate certain frequencies. Unlike active filters, which employ amplifying components like op amps, passive RC filters rely solely on resistors and capacitors.
The primary role of the resistor-capacitor combination is to selectively allow certain frequencies to pass through while suppressing others, contributing to the overall shaping of the signal without boosting its amplitude. The most you can get from a passive RC filter is what you put into it.
How Passive RC Filters Work
To better understand how an RC filter operates it’s best to revisit our old friend: the Voltage Divider. Just like passive RC filters, voltage dividers are built with passive components: two resistors. If you apply an audio signal to the input of a voltage divider, you will achieve a fixed version of the attenuator circuit.
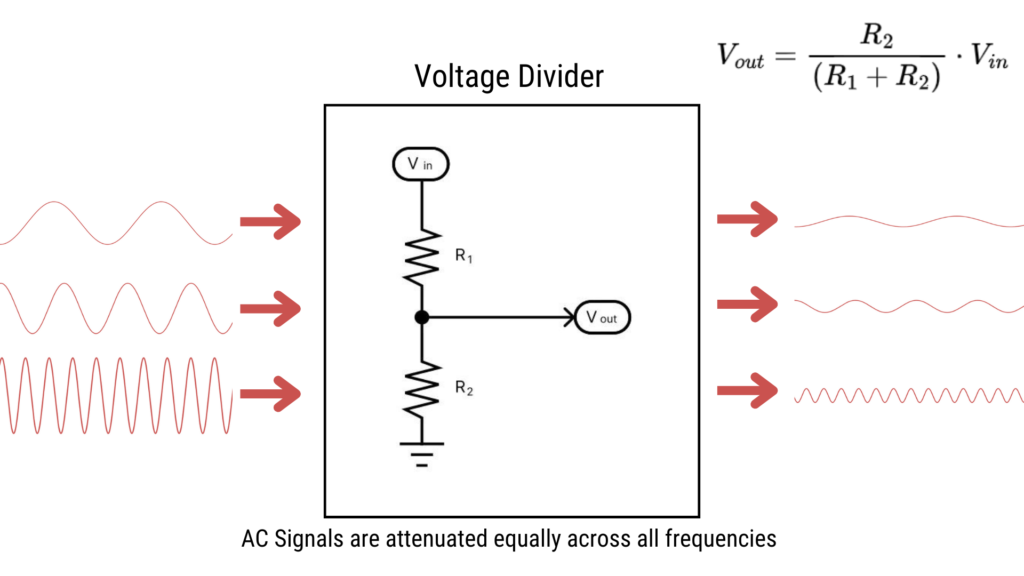
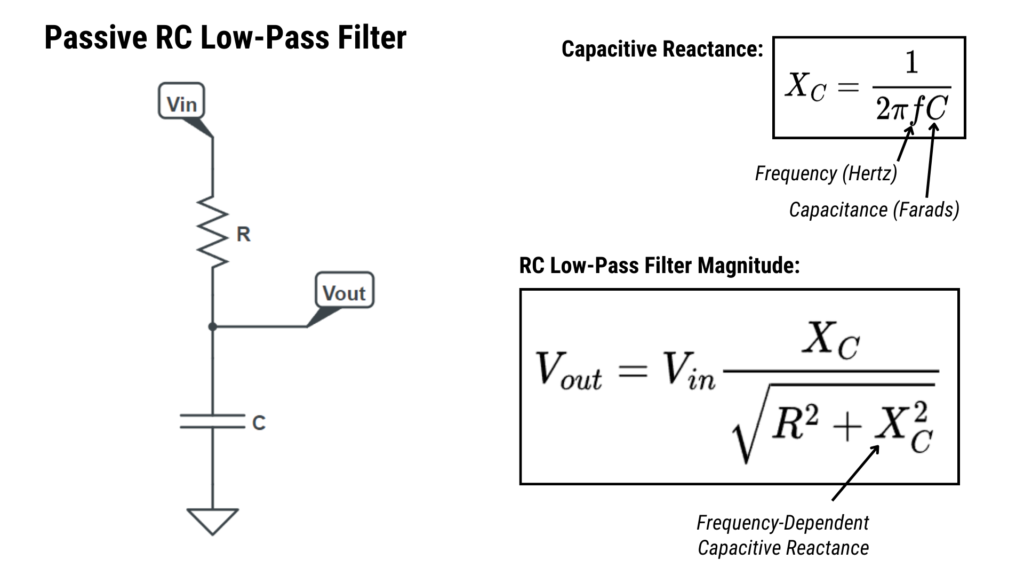
The Attenuator does not discriminate: it attenuates all frequencies equally. If we replace one of the resistors with a capacitor the attenuation becomes frequency-selective. That’s because capacitors have a property called reactance (XC), which is defined as the opposition that a capacitor presents to an AC signal. Capacitive reactance is a frequency-dependent property of all capacitors, and that is the primary reason why RC filters are frequency-dependent.
Figure 12.4 shows the RC low-pass filter in the same topology as the voltage divider circuit above, with R2 replaced by a capacitor. It shows how the output signal amplitude (Vout) can be calculated based on the input signal’s amplitude (Vin) and frequency (f).
How to Design a Passive RC Filter
1. Define the Filter Type and Cut-Off Frequency
First, you need to define the type of filter you want to build. In our case, there are two options: low-pass and high-pass. Remember, low-pass filters attenuate frequencies higher than the cut-off frequency. Alternatively, high-pass filters attenuate frequencies lower than the cut-off frequency.
Evidently, you will also need to define the cut-off frequency in Hertz. Common cut-off frequency values lie between the audio frequency band, which ranges between 20 Hz and 20 kHz.
For example, let’s choose to design a low-pass filter with a cut-off frequency of 110 Hz, which is the same frequency as the ‘A’ string on guitar in standard tuning. Applying this filter should create a muffled, bass-y sound.
2. Calculate Component Values
Second, we need to calculate the resistor and capacitor values. The cut-off frequency can be calculated using Equation 12.1. The same equation rearranged to solve for resistance is shown in Equation 12.2.
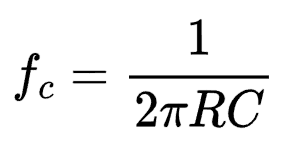
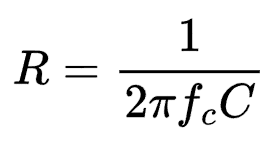
If you start with a capacitance value in mind, you can easily calculate the corresponding resistance value using Equation 12.2. For example, let’s assume we use a 1µF capacitor. Our desired cut-off frequency is 110 Hz, which yields a resistance of 1.447 kΩ.
Now, part of this process is to come up with realistic component values. As you can imagine, 1.447 kΩ is not a standard resistor value. The industry-standard resistance values are based on a numbering scheme called the E series of preferred numbers. The most common E series values fall into the E12 and E24 scheme, so the closest practical industry-standard for our case is 1.5kΩ.
With a 1.5kΩ resistor and 1µF capacitor, using Equation 12.1 gives us an expected cut-off frequency of 106 Hz. That’s within 5% of what we’re after, which is acceptable for our case.
3. Build and Test
Now that you’re finished with the preliminary design, you can prototype it and see if it works! We’ll be using the handy PROTIS 1 MINI Development Board to breadboard the circuit and we’ll test it out with real audio.
Figure 12.6 shows a RC low-pass filter circuit built on the PROTIS 1 MINI board. The components used are 1.5kΩ 1% metal-film resistor and a 1µF electrolytic capacitor. I recorded some before and after audio for you to hear how much of a difference the filter makes.

The audio below exhibits the “clean” guitar signal with the PROTIS 1 MINI bypassed. I’m playing through a Telecaster-style Cole Clark electric with the pickup switch in the center position.
And the following clip was taken after the signal passes through the RC low-pass filter. You’ll notice that the tone is not quite as hot. That’s because the volume was been reduced substantially. The higher notes in the take are only audible because I recorded the track with the guitar in the room. The higher end coming through the actual amplifier is extremely attenuated.
From Passive to Active Filtering
You may have noticed that the “after” audio sample was considerably lower volume than the “before” counterpart. As mentioned earlier, RC filters are passive circuits and therefore do not add gain. As such, they can act as leeches on your tone. No worries though, we will be going over active approaches for building RC filters in future articles. This will arm you with the tools needed to buffer your signal and retain your instrument’s character.
You may also be wondering why passive filters are used at all in guitar pedals, seeing that they suck so much from the signal. The reason is because most RC circuits are used in conjunction with gain-producing circuits. For example, a passive filter might be placed after a gain stage in an overdrive circuit. Since the gain is already high, a little attenuation won’t hurt.
Guitar Effects Design in 48 Circuits or Less
The 48 Circuits or Less article series serves to close the gap between DIY guitar effects design and guitarists interested in the craft by uniquely curating the most important aspects of DIY guitar effect circuit design. This post is part of the 48 Circuits or Less series. View more articles in this series here.
Meet the Author:

Hi, I’m Dominic. By day, I’m an engineer. By night, I repair and modify guitar effects! Since 2017, I’ve been independently modifying and repairing guitar effects and audio equipment under Mimmotronics Effects in Western New York. After coming out with a series of guitar effects development boards, I decided the next step is to support that community through content on what I’ve learned through the years. Writing about electronics gives me great joy, particularly because I love seeing what others do with the knowledge they gain about guitar effects and audio circuits. Feel free to reach out using the contact form!
The Tools I Use
As a member of Amazon Associates, Stompbox Electronics earns and is supported by qualifying purchases.














